Filetype PDF | Posted on 26 Jan 2023 | 2 years ago
Authentication
digital resources
100x Filetype PDF File size 0.19 MB Source: www.math.drexel.edu
Partial Derivatives
SUGGESTEDREFERENCEMATERIAL:
Asyouworkthroughtheproblemslistedbelow, youshouldreference Chapter 13.3 of the rec-
ommendedtextbook(ortheequivalent chapter in your alternative textbook/online resource)
and your lecture notes.
EXPECTEDSKILLS:
• Be able to compute first-order and second-order partial derivatives.
• Be able to perform implicit partial differentiation.
• Be able to solve various word problems involving rates of change, which use partial
derivatives.
PRACTICEPROBLEMS:
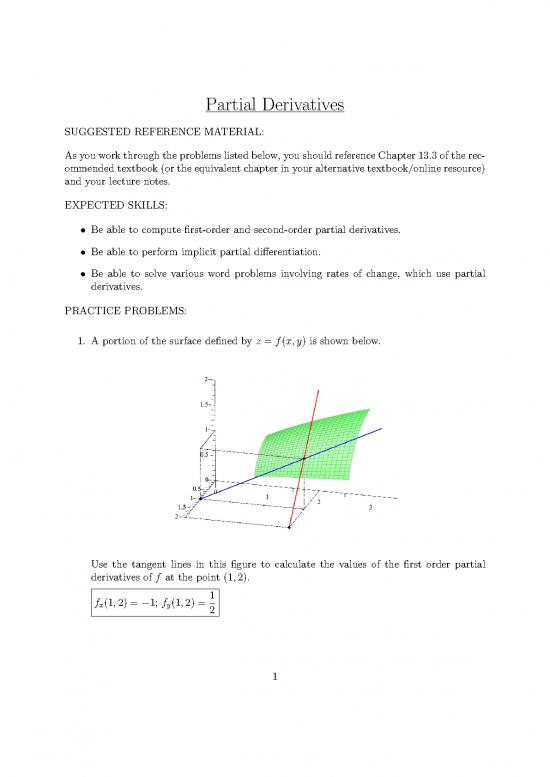
1. A portion of the surface defined by z = f(x,y) is shown below.
Use the tangent lines in this figure to calculate the values of the first order partial
derivatives of f at the point (1,2).
f (1,2) = −1; f (1,2) = 1
x y 2
1
For problems 2-9, find all first order partial derivatives.
2. f(x,y) = (3x−y)5
f (x,y) = 15(3x−y)4; f (x,y) = −5(3x−y)4
x y
3. f(x,y) = exsiny
f (x,y) = exsiny; f (x,y) = excosy
x y
4. f(x,y) = tan−1(4x−7y)
f (x,y) = 4 ; f (x,y) = − 7
x 2 y 2
1+(4x−7y) 1+(4x−7y)
5. f(x,y) = xcos(x2 +y2)
f (x,y) = cos(x2 +y2)−2x2sin(x2 +y2); f (x,y) = −2xysin(x2 +y2)
x y
p 2 2 ∂f ∂f ∂f
6. Let f(x,y,z) = x −2y+3z . Compute ∂x, ∂y, and ∂z.
∂f = p x ; ∂f = p −1 ; ∂f = p 3z
∂x x2 −2y+3z2 ∂y x2 −2y+3z2 ∂z x2 −2y+3z2
7. Let w = 4z . Compute ∂w, ∂w, and ∂w.
x2 +y2 ∂x ∂y ∂z
∂w =− 8xz ; ∂w = − 8yz ; ∂w = 4
2 2 2 2 2 2 2 2
∂x (x +y ) ∂y (x +y ) ∂z x +y
8. Consider f(x,y,z) = xy . Determine ∂f(−1,1,2), ∂f(−1,1,2), and ∂f(−1,1,2).
x2 +z2 ∂x ∂y ∂z
∂f 3 ∂f 1 ∂f 4
= ; =− ; =
∂x 25 ∂y 5 ∂z 25
(x,y,z)=(−1,1,2) (x,y,z)=(−1,1,2) (x,y,z)=(−1,1,2)
2 π π π
9. Suppose f(x,y,z) = z sin(2xy). Compute f 4, , 1 , f 4, , 1 , and f 4, , 1 .
x 3 y 3 z 3
π π π π √
f 4, , 1 =− ,f 4, ,2 =−4,f 4, ,2 = 3
x 3 3 y 3 z 3
For problems 10-11, find all values of x and y such that f (x,y) = 0 and f (x,y) = 0
x y
simultaneously.
10. f(x,y) = 4x2 +y2 −8xy +4x+6y−10
(x,y) = 7, 5
6 3
2
11. f(x,y) = x2 +4y2 −3xy +3
(x,y) = (0,0)
For problems 12-13, compute all second partial derivatives.
12. z = x2y −y3x4
∂2z ∂2z ∂2z ∂2z
2 3 3 2 3 2 4
∂x2 = 2y −12x y ; ∂y∂x = 2x−12x y ; ∂x∂y = 2x−12x y ; ∂y2 = −6x y
13. f(x,y) = ln(x2 +3y)
−2x2+6y 6x
f (x,y) = ; f (x,y) = − ;
xx 2 2 xy 2 2
(x +3y) (x +3y)
f (x,y) = − 6x ; f (x,y) = − 9
yx 2 2 yy 2 2
(x +3y) (x +3y)
14. Consider the surface S : z = x2 + 3y2.
(a) Find the slope of the tangent line to the curve of intersection of the surface S and
the plane y = 1 at the point (1,1,4).
2; Detailed Solution: Here
(b) Find a set of parametric equations for the tangent line whose slope you computed
in part (a).
There are many possible parameterizations. One possibility is x = 1 + t, y = 1,
z = 4+2t. Detailed Solution: Here
(c) Find the slope of the tangent line to the curve of intersection of the surface S and
the plane x = 1 at the point (1,1,4).
6; Detailed Solution: Here
(d) Find a set of parametric equations for the tangent line whose slope you computed
in part (b).
There are many possible parameterizations. One possibility is x = 1, y = 1 + t,
z = 4+6t. Detailed Solution: Here
(e) Find an equation of the tangent plane to the surface S at the point (1,1,4). (Hint:
The tangent plane contains both of tangent lines from parts (b) and (d).)
−2(x−1)−6(y−1)+1(z−4)=0;Detailed Solution: Here
15. Consider a closed rectangular box.
(a) Find the instantaneous rate of change of the volume with respect to the width,
w, if the length, l, and height, h, are held constant at the instant when l = 3,
w=7,andh=6.
18
3
(b) Find the instantaneous rate of change of the surface area with respect to the
height, h, if the length, l, and width, w, are held constant at the instant when
l = 3, w = 7, and h = 6.
20
16. Use implicit partial differentiation to compute the slope of the surface x2+4y2−36z2 =
−19 in the x-direction at the points (1,2,1) and (1,2,−1).
∂z 1 ∂z 1
= ; =−
∂x 36 ∂x 36
(x,y,z)=(1,2,1) (x,y,z)=(1,2,−1)
17. Compute ∂z and ∂z if xcos(y2 +z2) = 3yz.
∂x ∂y
∂z cos(y2 +z2) ∂z −3z−2xysin(y2+z2)
∂x = 3y +2zxsin(y2 +z2); ∂y = 3y +2xzsin(y2 +z2) ; Detailed Solution: Here
18. Laplace’s Equation, shown below, is a second order partial differential equation. In
the study of heat conduction, the Laplace Equation is the steady state heat equation.
Laplace’s Equation:
2 2
d f + d f = 0
2 2
dx dy
Afunction which satisfies Laplace’s Equation is said to be harmonic.
(a) Verify that f(x,y) = excosy is a harmonic function.
You can verify by direct computation that f (x,y) = excosy and f (x,y) =
xx yy
−excosy. Then, f (x,y) + f (x,y) = excosy + (−excosy) = 0. Thus, since
xx yy
f(x,y) satisfies Laplace’s Equation, it is a harmonic function.
(b) Suppose u(x,y) and v(x,y) are functions which have continuous mixed partial
derivatives. Also, assume that u(x,y) and v(x,y) satisfy the Cauchy Riemann
Equations:
∂u = ∂v
∂x ∂y
∂u =−∂v
∂y ∂x
Verify that u(x,y) and v(x,y) are both harmonic functions.
4
no reviews yet
Please Login to review.
